Tagged Data

Introduction to Tagged Data

Before we can create generic operators, we first have to be able to keep track of data types. Why?

Think back to Lesson 4 where we implemented rational numbers. We made the decision to store rational numbers as a pair, where the car held the numerator and the cdr held the denominator. Meanwhile, our frenemy, Ben Bitdiddle, implemented complex numbers. He represented these numbers as a pair as well: the car held the real part and the cdr held the imaginary part.

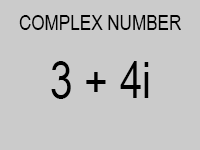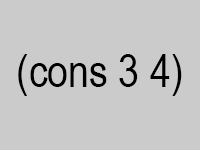
Now, given a pair whose car is 3 and whose cdr is 4, how can we tell if the given data represents the rational number [mathjaxinline]\frac{3}{4}[/mathjaxinline] or the complex number [mathjaxinline]3+4i[/mathjaxinline]? The raw data we are given can be interpreted either way, so we can't know for sure! In fact, the pair may be neither of the two and actually represent some other data type. That's why need a system to associate data with their particular types.

(Side note: At this point, you might be mad at Ben—why did he have to use the same representation as us?! However, he really isn't to blame. Even if he used a different internal representation, we cannot use this distinction to check the type of the data: we would be breaking data abstraction barriers!)

The solution is to have tagged data: Each piece of data carries around information about its type. We can do this by attaching tags to all our data. To accomplish this, we need a constructor to tag our data (attach-tag) and selectors to grab the tag and the data from a piece of tagged data (type-tag and contents).

Here's a possible implementation for handling tagged data.

(define (attach-tag tag data)
  (cons tag data))

(define (type-tag tagged-data)
  (if (pair? tagged-data)
      (car tagged-data)
      (error "Not tagged data")))

(define (contents tagged-data)
  (if (pair? tagged-data)
      (cdr tagged-data)
      (error "Not tagged data")))

Can you come up with another set of constructors and selectors that implements data tagging using a different internal representation?

Tagging Rational and Complex Numbers

Now that we've implemented tagged data, we can fix our implementations of the rational and complex number data types. Our old code looked like this:

(define (make-rational numer denom)
  (cons num denom))

(define (make-complex real imag)
  (cons real imag))

But now we can do this:

(define (make-rational numer denom)
  (attach-tag 'rational (cons num denom)))

(define (make-complex real imag)
  (attach-tag 'complex (cons real imag)))

Notice that we easily could have replaced the function attach-tag with cons and the code would have still worked. But this violates the data abstraction barrier we created!

We can then write selectors using contents. For example, for rational numbers:

(define (numer n)
  (car (contents n)))

(define (denom n)
  (cdr (contents n)))

Writing Procedures for Tagged Data

Our goal is to write a universal addition procedure. It should work with rational numbers and complex numbers.

The first step is to write addition procedures that are specific to the data types of the inputs. Using the constructors and selectors that we just wrote in the previous section, this should be fairly straight forward.

Try the following:

1. Write add-rational, which takes in two rational numbers and returns a rational number equal to the sum of the two inputs. Remember to respect the data abstraction by using proper constructors and selectors.

2. Write add-complex, which takes in two complex numbers and returns a complex number equal to the sum of the two inputs. Remember that [mathjaxinline](a+bi) + (c+di) = (a+c)+(b+d)i[/mathjaxinline].

3. Assume that we've written a procedure add-rational-complex which takes in rational number and complex number in that order, and adds them properly.

4. Now write a generic addition operation called add-numbers that takes in two numbers, each of which can be either rational or complex. We should rely on tags to direct our data to the correct procedure above.

Check your answers below.

Solutions

Your add-rational should look something like this:

(define (add-rational x y)
  (make-rational (+ (* (numer x) (denom y))
                    (* (numer y) (denom x)))
                 (* (denom x) (denom y))))

Your add-complex should be similar. Notice that we didn't have to worry about tagging, thanks to the abstraction barrier created by make-rational, numer, and denom.

Now for add-numbers:

(define (add-numbers num1 num2)
  (cond ((and (equal? (type-tag num1) 'rational)
              (equal? (type-tag num2) 'rational))
         (add-rational num1 num2))
        ((and (equal? (type-tag num1) 'complex)
              (equal? (type-tag num2) 'complex))
         (add-complex num1 num2))
        ((and (equal? (type-tag num1) 'rational)
              (equal? (type-tag num2) 'complex))
         (add-rational-complex num1 num2))
        (else
         (add-rational-complex num2 num1))))

Great! We can now add numbers using a single generic procedure!

Reflection

Let's think about what we've learned:

1. We don't even need to know how tags are implemented to write this add-numbers! This is because we properly abstracted away those details. So we can just use the selector type-tag to tell us what type of data we're dealing with.

2. If we want to add another type of number to our system, we'll have to change our generic function's definition, adding a good number of extra conditions to handle the new data type. The modifications would be straightforward in our situation, but this wouldn't work with larger systems. In other words, our system has poor scalability.

Although the add-numbers example is a little contrived, there are many systems that do use tagged data in the real world. In fact, the Racket interpreter uses tagged data to evaluate your code!

Weaknesses of Tagged Data

As we hinted above, tagged data systems have several key weaknesses.

One weakness is that every data type must be identified and manually incorporated into every generic procedure. For instance, suppose we wanted to incorporate a new type of number into our system. We would need to identify this new representation with a type, then edit all the generic procedures out there (add-numbers, multiply-numbers, divide-numbers, etc.) to check for the new type and carry out the appropriate operations.

Another weakness is that even though the individual representations and corresponding procedures can be designed separately, we must guarantee that no two procedures in the entire system have the same name. This is why we created the new procedure add-numbers, which calls add- rational, add-complex, and add-rational-complex.

The issue underlying both of these weaknesses is that the technique for implementing generic interfaces does not scale—the person implementing the generic procedures must modify those procedures each time a new representation or type is added. Additionally, the people who originally wrote the rational number system and the complex number system must now modify their code to avoid name conflicts. In each of these cases, the changes that must be made to the code are straightforward, but they must be made nonetheless, and this is a source of inconvenience and error.