Hierarchical Structures - Capital-T Trees

Intro to Capital-T Trees (The Abstract Data Type)

Before you continue reading, note that the capital-T Trees we talk about in this section are different than the trees from SICP. In SICP (and in the previous sections), trees are simply a fancy word for deep lists. In this section, we introduce a new concept, Trees, which are an abstract data type (ADT). These Trees must respect certain abstraction barriers. When you hear most computer scientists talk about Trees in the real-world, they are typically talking about this ADT.

As with lists and sentences, we can also store data in the Trees data structure. They are generally useful for providing hierarchy, ordering, and composition.

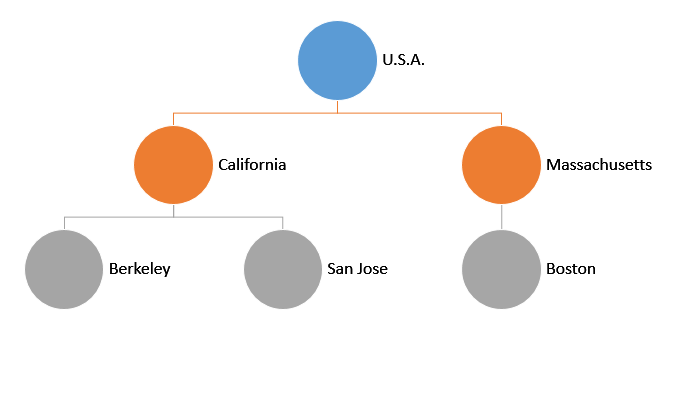
The name comes from the downwards branching structure, similar to real trees but upside down. A node is a point at the Tree. Each node contains a datum ("U.S.A", "California" are some datums). Notice that a node can contain another Tree. The node with "California" can be regarded as a Tree with "California" at the top. Because of this, nodes and Trees are the same thing! We generally use 'Tree' to refer to the whole structure. Another synonym for a node is subtree.

• The root of a Tree is the topmost node. All Trees have only one root. In this case, it is "U.S.A"
• The parent of a node is the node directly above it. All nodes have exactly one parent, except for the root which has no parent.
• The children of a node are the nodes that are directly beneath it. The children of "California" are "Berkeley" and "San Jose".
• A branch node is a node that has at least one child (like "U.S.A","California" and "Massachusetts").
• A leaf node is a node that no children. (like "Berkeley", "San Jose", and "Boston")

The Tree ADT

We have our own ADT to represent Trees that we will use for the rest of this lesson, but there is no official way to represent Trees. Why? This is because there are several different design choices to make when creating a Tree ADT:

• Branch nodes may or may not have data
• Binary Trees (2 branches) vs N-way Trees (N branches)
• Order of children
• Can Trees be empty?
• ... and many more

Different representations of Trees will give you different limitations, features, and functionalities.

Here are the built-in constructors and selectors for Trees:

• Constructor: make-tree takes in two arguments, a datum and a list of its children, and creates a Tree ADT.
• Selector: datum takes in a node and returns the datum that the node stores.
• Selector: children takes in a node and returns the list of its children.

Under the Hood

One way to implement the Trees described above is with the following definitions:

(define (make-tree datum children) 
  (cons datum children))
(define (datum node) 
  (car node))
(define (children node) 
  (cdr node))

The selector children accepts a node as its single argument and returns its children, a list of Trees. A list of Trees is called a forest. Remember that Trees and forests are two different data structures! In addition, you should think of a forest as a list of Trees, but you should NOT think of a Tree as a bunch of cons, cars, and cdrs.

To reiterate, the constructor and selectors for forests are list, car, and cdr, while the constructor and selectors for (this ADT of) Trees are make-tree, datum, and children.

Additionally, since a leaf is a node with no children, we could use a predicate like this to check whether a node is a leaf:

(define (leaf? node)
  (null? (children node)))

Remember that using lists is just one way to represent Trees. We can't assume that someone who designed the ADT would use a list. For example, if maple is a Tree, we can't assume that (cdr maple) will give us the children. Instead, we must respect the data abstraction and use the constructors and selectors they provide for us.

Abstraction Barrier

We cannot stress enough that you cannot make any assumptions on how a Tree ADT is implemented. When working on Trees, you can only use the constructors/selectors that are provided. Since forests are implemented as a list of Trees, you can use car of a forest to find the first Tree, or cdr to find a list of the rest of the Trees.

Mapping over Trees

Something useful that we do to Trees often is to map a certain operation to it, akin to mapping over a list. We can achieve this by the following:

(define (treemap fn tree)
   (make-tree (fn (datum tree))
              (map (lambda (t) (treemap fn t))
                   (children tree) )))

We apply the function to our datum, and map the function recursively on the children.

Make sure you stare at the above code until it makes sense.

Mutual Recursion

Here is an alternative way to define treemap that applies a function fn throughout the tree. Observe how the overall process is recursive, but treemap does not directly call itself. treemap will be (mostly) responsible for applying fn to the datum of a single Tree. Who handles the forest? Well, treemap will call a helper procedure, forest-map, which applies fn to all elements in the forest.

(define (treemap fn tree)
    (make-tree (fn (datum tree))
               (forest-map fn (children tree))))

How does forest-map apply fn to the forest? Well, a forest is just a list of Trees, and we know that we have treemap that handles a single Tree. So, all we need to do is recursively call treemap on all Trees in the forest!

(define (forest-map fn forest)
    (if (null? forest)
        '()
        (cons  (treemap fn (car forest))
               (forest-map fn (cdr forest)))))

Notice that treemap calls forest-map, and forest-map calls treemap. The pattern of A calling B and B calling A is called mutual recursion.

count-leaves

Let's use mutual recursion to write the procedure count-leaves, which returns the number of leaves in a tree. Let's take this step by step. Since we're using mutual recursion, that means we'll need a procedure to manage Trees, count-leaves, and a procedure to manage forests, count-leaves-in-forest.

count-leaves:

• Base case: If the node is a leaf node, then just return 1.
• Recursive call: Otherwise, it calls count-leaves-in-forest.

Here is the code for count-leaves:

(define (count-leaves tree)
  (if (leaf? tree)
      1
      (count-leaves-in-forest (children tree))))

count-leaves-in-forest:

• Base case: If the forest is null?, return 0.
• Recursive call: Otherwise, we need to find the total number of leaves in all of the trees in the forest.
  1. We call count-leaves on the car of the forest to find how many leaves are in the first Tree of the forest.
  2. We recursively call count-leaves-in-forest on the cdr of the forest to find the number of leaves in the rest of the forest.
  3. Finally, we add these two values together to find the total number of leaves.

Here is the code for count-leaves-in-forest:

(define (count-leaves-in-forest forest)
  (if (null? forest)
      0
      (+ (count-leaves (car forest))
         (count-leaves-in-forest (cdr forest)))))

Tree Traversals

We have seen how we can store and find elements in Trees. Now, many situations that use the Tree data structure involves visiting all of our nodes and do something with all of the elements. The obvious way is to go up-down and left-right, but there are many other ways we can traverse a Tree.

Depth First Search

Depth First Search (DFS) is when you explore a node's children before its siblings. The name comes from the fact that you are going as deep as you can in one branch before looking at other branches. The gif below demonstrates this. The numbers indicate the order in which the nodes are visited.

Note that it finishes exploring one branch before exploring other branches.

We can demonstrate this in Racket. Lets say we want to print every single node. Our Tree ADT actually follows the same structure, so our implementation of dfs is rather simple:

(define (depth-first-search tree)
    (print (datum tree))
    (for-each depth-first-search (children tree)))

Breadth First Search

Breadth First Search (BFS) explores the siblings before its children. It's easier to imagine this as looking at the graph in 'layers'. First we look at the Tree's root, then its children, followed by its grandchildren, and so on. The gif below demonstrates this:

Implementing BFS in Racket is slightly harder because our ADT stores information in a different order than the order in which BFS traverses. One way around this is to use another data structure called a queue, which stores (in order) the nodes that are going to be checked next.

(define (breadth-first-search tree)
    (bfs-iter (list tree)))

(define (bfs-iter queue)
    (if (null? queue)
        'done
        (let ((task (car queue)))
            (print (datum task))
            (bfs-iter (append (cdr queue) (children task))))))

BFS Example

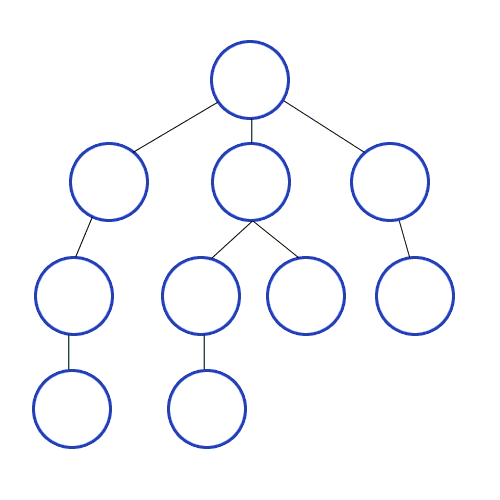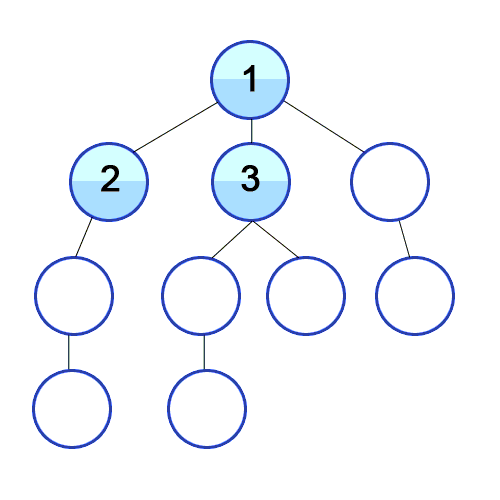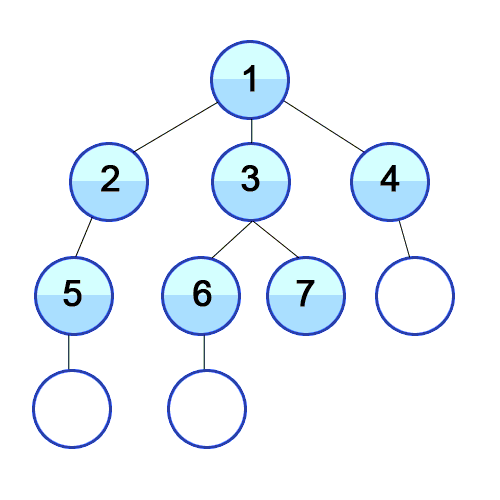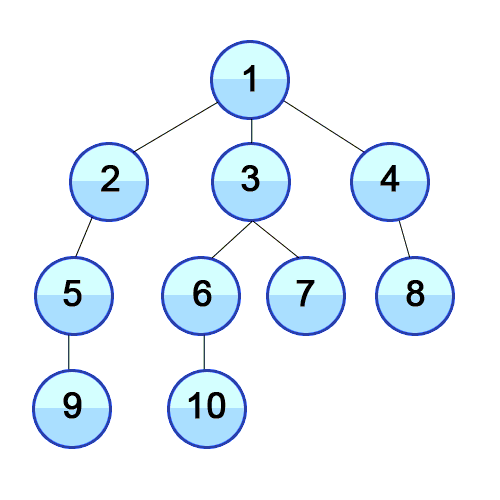
Lets walk through how the code above works using the example Tree below. The arrows in the diagram indicate the parent --> child relationships.

When bfs-iter is first called, the whole Tree is put into the queue. To simplify things, let's say a tree is denoted by its root.

queue: F

It dequeues node F, prints the value of node F, and recursively calls bfs-iter with the rest of the queue and the children of F. The rest of the queue is empty, but the children of F is B G.

queue: B G

bfs-iter will print the node of the first tree in the queue, B and recursively calls bfs-iter with the rest of the queue, G, and the children of B, A D.

queue: G A D

And so on until the queue is empty. Once the queue is empty, we will have printed out each node's datum exactly once.

Note that the siblings are always first in the queue and the children are entered from the back. This ensures that siblings are checked first before children.

DFS vs BFS

Is one better than the other? It depends on what you are trying to do with your Trees and how you are storing elements in the Tree.

The Tree below represents things in a house. In a "House" you can find a "Kitchen" and "Cat Food". In a "Kitchen" you can find a "Drawer", "Trash Can", etc. The leaves contain food and the deeper you go, the more filling the foods are.

Takeaways

Here are the takeaways from this subsection:

• Remember your constructor and selectors (make-tree, datum, and children).
• To map over Trees, we use mutual recursion, where the two procedures are written in terms of each other. Typically, one of those procedures takes in a Tree, and the other takes in a forest.
• Breadth First Search looks at the nodes in the same level first, whereas Depth First Search goes through each branch until it hits the leaf node.